
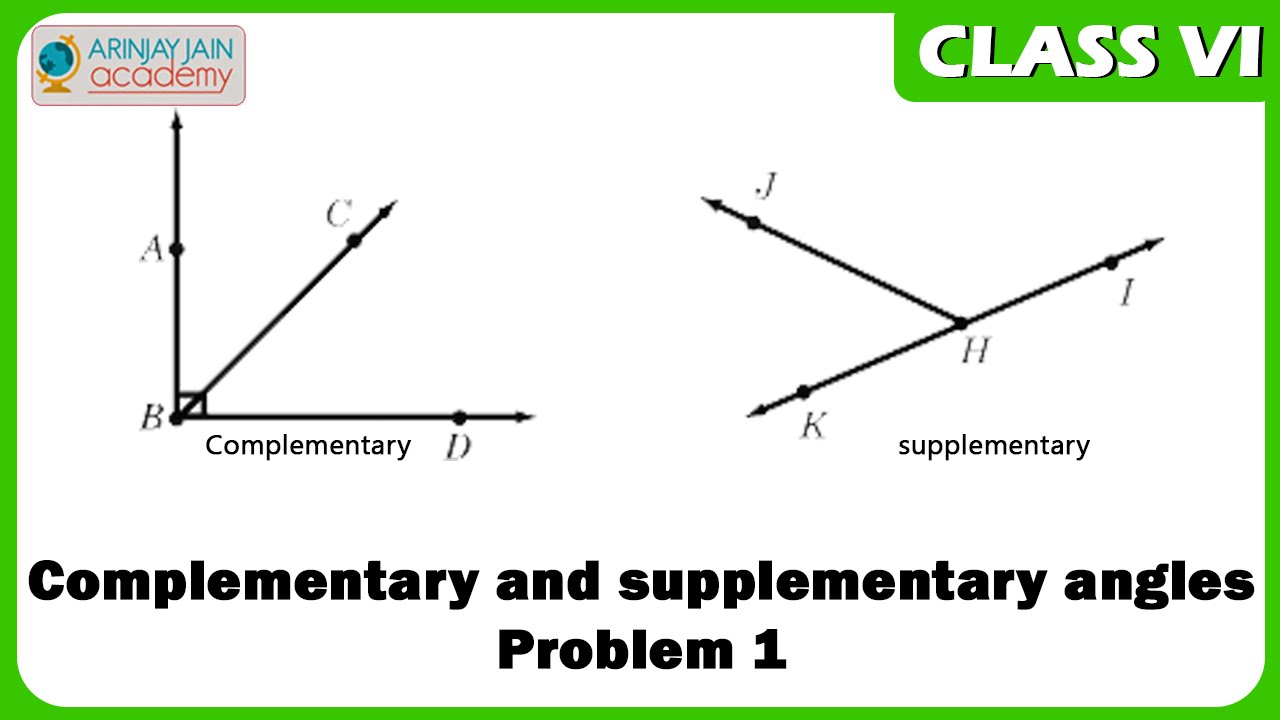
Adjacent angles can help prove that lines are parallel.

These are all examples of adjacent angles. Not only does this construction form eight pairs of angles (adjacent angles), but all those pairs are also linear pairs! Which angles are adjacent angles? Where the transversal cuts across them, we have points H and U: Parallel lines and a transversal Here are parallel lines CP and MN cut by transversal IK. Did you identify ∠A as the common vertex? Parallel lines and transversals See if you can identify the common side and common vertex: Adjacent angles creating linear pair The sum of their angles is 180° or π radians.Īngles that sum to 180° are called supplementary angles. When a pair of adjacent angles create a straight line or straight angle, they are a linear pair. Angles ∠ZWI and ∠HWI are adjacent angles. Notice both those angles share a common vertex at Point W, and a common side, line segment WI. This creates two additional angles at Point W:
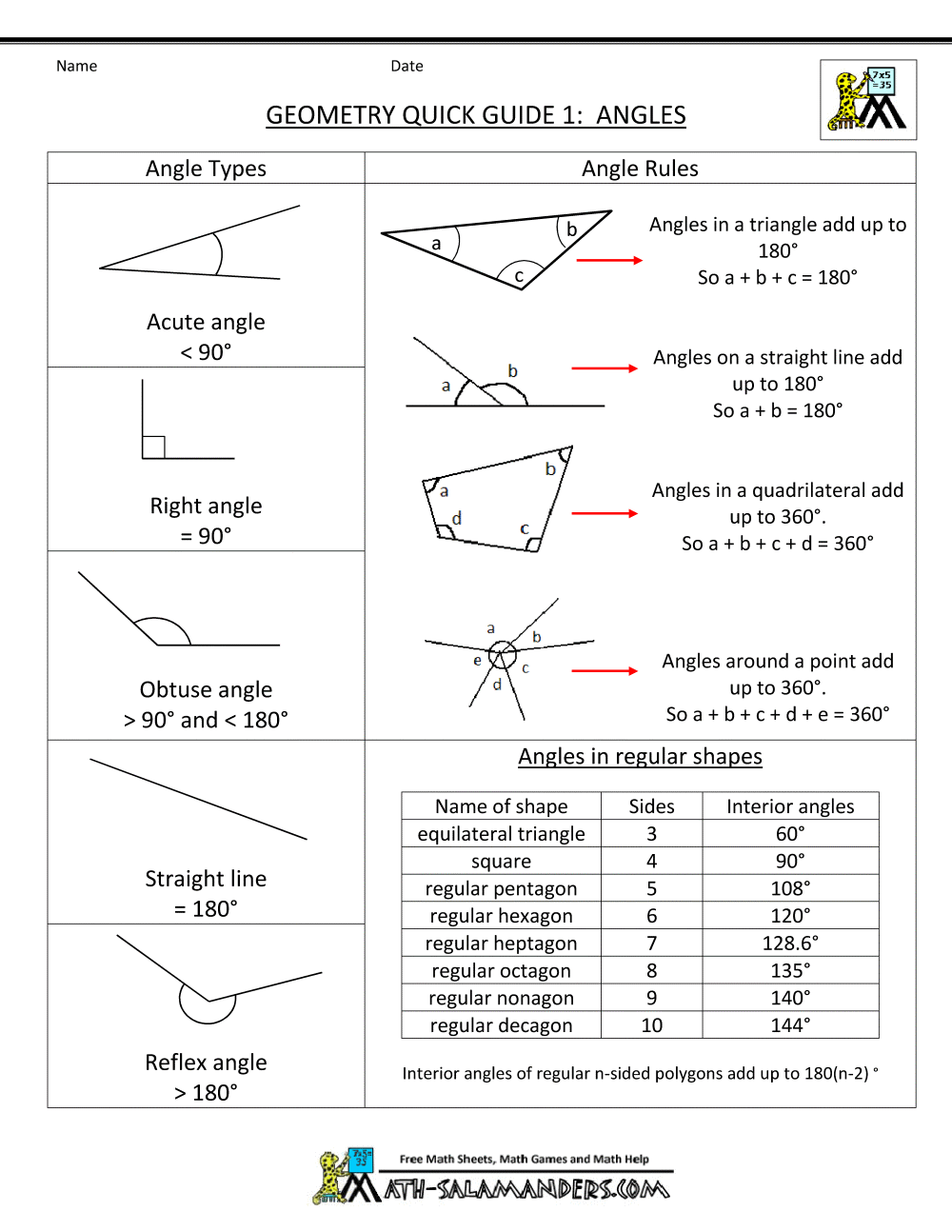
If we connect Point W with Point I, we construct diagonal WI. Here we have a simple square formed by four sides creating four vertices: ∠W, ∠H, ∠I, and ∠Z. Let's see how one vertex of a square can demonstrate adjacent angles. What is a common side in geometryĪdjacent angles are always pairs and never overlap. Both angles use the common side and one other side. What is a common side in geometry?Ī common side is one line, ray, or line segment used to create two angles sharing the same vertex. You see vertices in the corners of polygons, as central angles in circles, and when linear constructions, like parallel lines and transversals, cross. You can mix and match these to create vertices (the plural of vertex) in many ways: What is a common side in geometry A vertex is the point at the intersection of any two linear constructions.
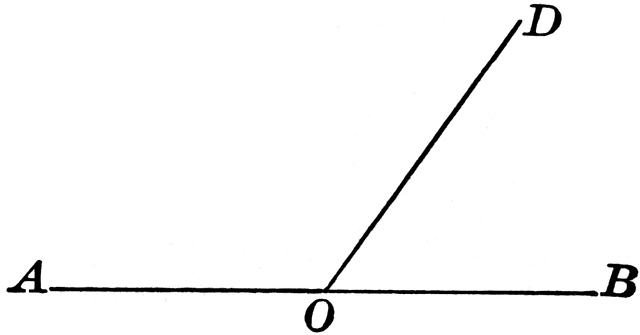
What is a common vertex?Ī common vertex is a vertex that is shared by two angles. Vertical angles are a pair of opposite angles made by two intersecting lines. If the two angles only share a common vertex, then they are vertical angles. The letter ‘c’ in complementary comes before the letter ‘s’ in supplementary, just like 90° comes before 180°.Three features make adjacent angles easy to pick out:.Hence when two supplementary angles are put together they form a ‘straight’ angle. The letter‘s’ for ‘supplementary’ and‘s’ for ‘straight’.Hence when two complementary angles put together to form a ‘corner right’ angle. The letter ‘c’ for ‘complementary’ and ‘c’ for ‘corner’.Then, by the definition of supplementary angles,Ĭomplementary vs Supplementary Angles Complementary AnglesĮach participating angle is complement of the otherĮach participating angle is supplement of the other Let ∠POB is supplementary to ∠AOP and ∠QOB If they are adjacent they will form a straight angle. Similar to complementary angles, the two angles do not need to be adjacent. The word ‘supplementary’ came from the Latin word ‘supplere’ meaning ‘supply’. Each angle in the pair is said to be the supplement of the other. Two angles are called supplementary angles if the sum of their measure equals 180°. A staircase that have an escalation of 30° and the wall at 90°.Hands of a clock showing 3PM and the seconds hand pointing towards the digit 2.When a rectangular piece of bread is divided into two pieces by cutting along the diagonal, we get two right triangles, each with a pair of complementary angles.Hence Proved Real Life Examples of Complementary Angles Then, by the definition of complementary angles, Let ∠ZOW is complementary to ∠XOZ and ∠YOW


 0 kommentar(er)
0 kommentar(er)
